When I was first learning about the technique of zodiacal releasing in the works of Vettius Valens, I was surprised to learn that Valens used a “year” of 360 days to time the unfolding of the various periods. His system is apparently an idealized version of a year (one complete cycle of the sun around the earth) in which each “day” corresponds to one degree of a circle, and each month is exactly 30 days.
This is the relevant passage from Valens discussion of zodiacal releasing (Mark Riley’s translation, italics mine):
“Since the universal year has 365 1/4 days, while the year with respect to the distribution has 360, we subtract the 5 1/4 intercalary days, then we find the number of years. Only then will we make the distribution.”
“For example: a person in his 33rd year was born on Tybi 15; we are investigating Mesori 20 of his 33rd year. I multiply 30 years times the 5 <intercalary> days for a total of 150. Now I add 10 <intercalary days> for the two complete years <31, 32> plus one-fourth of 32 (=8) for a total of 168. Next I take the number of days from Tybi 15 to the day in question, Mesori 20 (=215), and I add this amount to 168 for a grand total of 383. From this sum I subtract 360, and the remainder is 23. So the nativity will be in its 33rd full year with respect to the distribution, plus 23 days. I consider this number of years and days when making the distribution of the chronocratorships.”
Let’s analyze Valens’ example, using 5.25 intercalary days per “year”:
A man is in his 33rd year of life. He was born on Tybi 15, and we are investigating Messori 20 of his 33rd year. There are 215 days from Tybi 15 to Mesori 20.
Valens multiplies 30 years times the 5.25 <intercalary> days for a total of 157.5 days. (This accounts for the first 30 full years of life.)
Next he adds 10.5 <intercalary days> for the two complete years <31, 32> plus one-fourth of 32 (=8) for a total of 168.
- First 30 years => 157.5 intercalary days.
- Years 31 and 32 => 10.5 intercalary days.
- The total up to age 33 is 157.5 + 10.5 = 168 days.
- 215 days from Tybi 15 to Mesori 20 PLUT 168 days = 383 days total from the date of birth.
- 383 days minus 360 = 1 “year” and 23 days, that is, 33 “years” and 23 days.
To use a modern example, suppose someone is born on 01 Jan 1967 and turns 33 on 01 Jan 2000. The date 215 days after his 33rd birthday is 03 Aug 2000 in the tropical calendar. However, 33 “years” plus 23 days takes us to 24 Jan 2000, which is when Valens would make the distribution.
Interestingly, Valens system of “zodiacal releasing” is extremely similar to the Vedic method of nakshatra maha dashas (time periods ruled by planets). The nakshatra (moon mansions) dashas associate a certain sequence of planets to the moon’s mansions to determine which planet is the time-lord for a certain period of time. Each of the nakshatra dashas has a different ordering of planets which is paired to the nakshatras. You begin the counting with the nakshatra where the moon resides at birth and elect its associated planet as the time lord for the beginning of the dasha sequence. Each planet is assigned a number of years which it rules over, and you follow the sequence to find when the next planet will be activated. This is essentially the same method as Valens zodiacal releasing, except that the number of years allotted to each planet differs and in the Vedic system the releasing starts with the moon’s nakshatra’s associated planet rather than the Part of Spirit, which is Valens’ preferred starting point.
Another difference between Valens and Vedic practice is the length of the year. As mentioned above, Valens used a year of 360 days, yet modern Vedic astrologers seem to use the tropical or sidereal year, of 365.2422 or 365.2564 days respectively to time the periods allotted to the planets.
Interestingly, Vedic astrologer Vic DiCara has studied the ancient manuscripts in their original Sanskrit and has determined that the original “year” used in Vedic astrology was the so-called “nakshatra year” of about 359 days, based on one “day” being equal to one rotation of the earth against the fixed stars. This quite close to Valens 360 days, which is referred to in the Sanskrit literature as a ‘Savana’ year and is based on a day being measured from one sunrise to the next.
DiCara writes: “Surya Siddhanta calculates these practical timespans based entirely upon the revolution of the nakshatras through the sky (nakshatra ahoratra), which corresponds exactly to the rotation of the Earth on its axis. … Nakshatra time is the primary way of measuring how time allows events to occur in a particular sequence. It is to be used for anything and everything except what is specifically apportioned to the other systems. What is predictive astrology? It is an artful science of foretelling the sequence of events, portending how events will happen. Therefore what measurement system of time should be used for predictive astrology? The system that is specifically meant for defining how time causes events to unfold in sequence. What system is that? It is Nakshatra time. Therefore to calculate the duration of planetary eras and cycles you must use Nakshatra time, which defines a year as 359.017 days.”
How does DiCara arrive at 359.017 days for the length of a nakshatra year? Here is the math:
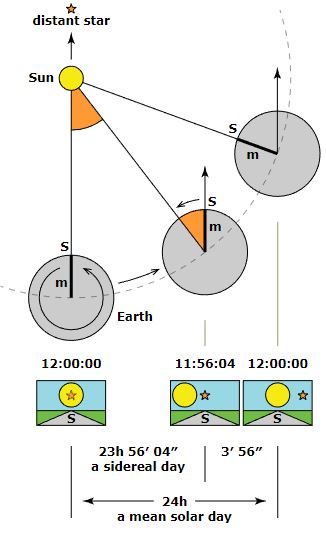
- A Savana day lasts exactly 24 hours.
- A nakshatra or sidereal day lasts 23.93446972 hours.
- The ratio of sidereal to Savana days is 23.93446972 divided by 24 = 0.997269572.
- Multiplying this ratio by the 360 degrees used by Valens for a perfect cycle gives 360 x 0.997269572 = 359.017 days.
In one of his videos, DiCara mentions that he has more precisely calculated this figure to be 359.0167 days in a nakshatra year, which was used in the ancient Vedic texts for predictive purposes in astrology.
In summary, it appears that Valens used an idealized “year” of 360 days for zodiacal releasing, based upon a complete cycle or circle having exactly 360 degrees and allowing each tropical day one degree of the circle.
The Vedic maha dasha system is similar, according to DiCara’s study of ancient texts, because each planet is also assigned a complete circle of 360 degrees as a “year,” but each degree of that circle corresponds to one sidereal day, which lasts 23.93446972 hours. Thus, one cycle (360 degrees) corresponds to 360 x 23.93446972 hours = 8616.409099 hours, which is equivalent to 359.017 tropical days (measured sunrise to sunrise).