This is the third post about the 5-degree rule in horary astrology, which Lilly adopted and used extensively in his practice. My hypothesis is that Lilly adopted this rule from Ptolemy’s discussion of how to calculate the length of life of the native. My question has to do with whether a technique developed to calculate the length of life in natal charts should also be applied to horary charts. If so, what is the theoretical rationale for doing so?
My investigation of this question has led to a discussion of Ptolemy’s method and the charts of early horary astrologers like Masha’allah and Sahl. In reviewing Ben Dykes translation of these authors, it appears that the use of both Whole Sign and quadrant houses was in effect in their time and that the 5-degree rule was variously applied. In his introduction (7c), Dykes notes:
“…Sahl recommends this 5-degree rule in a general way (not just in the context of longevity procedures, as Masha’allah does)…”
So it appears that there was a difference of opinion among these early horary astrologers about applying the 5-degree rule to other than length-of-life calculations.
In fact, in Chart 12 (a horary question about a rebellion in Africa) of On Reception Masha’allah ignores the 5-degree rule. Masha’allah’s text gives the position of Venus as 2 Sag 31, which is more than 5 degrees from the Ascendant, given as 8 Sagittarius (“the 9th degree of Sagittarius”), yet he specifically states the Venus is in the Ascendant and nowhere does Masha’allah mention the idea of Venus being cadent or lying in the 12th house, which suggests that he was using Whole Sign houses to analyze this chart. If Masha’allah were using quadrant houses, by the 5-degree rule Venus would have been considered a 12th house planet.
On the other hand, Wade Caves found a chart from Masha’allah in which he does use the 5-degree rule to include Mercury in the 10th house. This does not appear to be a horary chart, and I do not know if the issue being discussed was the length of life of the native (which would justify the use of the 5-degree rule) or some other topic. Here is the chart (I set the MC for Basra, Iraq, because the chart data are not available).

Here Mercury in the 9th sign Pisces lies about 2 degrees from the MC at 21 Pisces 30. Masha’allah writes, “Mercury is in its descent in the ninth, by equalization in the tenth.” When he says “in its descent in the 9th” it is not clear whether Masha’allah is using whole sign or quadrant houses because Mercury would be in the 9th in either system. When he writes “by equalization in the 10th” he must be referring to the 10th house because Mercury and Pisces are both in the 9th sign from the Ascendant, so here is is referring to quadrant houses with the cusp of the 10th being 21 Pisces 30. He apparently calls the use of the 5-degree rule here “equalization,” but what is being equalized?
My guess is that Masha’allah is referring to the Hellenistic concept found in Ptolemy of equalizing aspectual relationship in the ecliptic system with their counterparts in the mundane system. Ptolemy notes that aspects such as squares on the ecliptic can act like trines in signs of long ascension. Lilly himself adopted Ptolemy’s practice in this regard.
Masha’allah must have been aware of the Hellenistic use of Whole Sign houses in which the angular houses where those zodiacal signs in square (perpendicular) or in opposition to the Ascendant by whole sign. In a chart mentioned in a previous post, Masha’allah notes that “the cardines of the ascendant are perpendicular,” which implies that this is something special and not the norm. My hunch is that Masha’allah has in mind the difference between the angular whole sign houses which are always exactly perpendicular and the quadrant cardines (Angles) which are only perpendicular on a few specific occasions during the year.
In the mundane system the meridian and the horizon are perpendicular and their corresponding points on the ecliptic (Asc – Dsc axis, MC – IC axis) constitute the cusps of the angular houses. The angular houses (the power points in the chart) could differ in each system and needed to be “equalized” when interpreting a chart. If my analysis is correct, then the formula for the equalization becomes: zero degrees of of the Ascendant sign in the whole sign system equals the degree of the Ascendant minus 5 degrees in the quadrant house system and so for the other angles as well.
The following table may make this idea clearer. The Whole Sign house system is the idealized form of house division provided to us by the universe. The quadrant house system is particular to our location on Earth. How do we “equalize” the two systems (universal and particular) so that we can interpret their meaning in a birth chart?

Where does the 5 degree adjustment for quadrant houses come from? I believe it has to do with the Ascendant (eastern horizon of the chart) being a symbol of the life force of the native, which is derived from the Sun. The Ascendant of a chart derives its symbolism from the rising of the Sun.
The early astrologers based much of their interpretive theory on observation. We all know that the sun does not suddenly rise bringing about daylight, nor does it suddenly set, initiating the night. Sailors especially are aware of this phenomenon. For example, nautical lore distinguishes three types of twilight (and by implication three types of dawn). The following images from Wikipedia make this clear.

Notice in the above diagram that the sun sets at the horizon but there is an extended period after the moment of sunset during which the sun’s light gradually fades and the darkness of night completely dominates the scene. The astronomical measures of this gradual decline in available sunlight are shown in the next diagram.
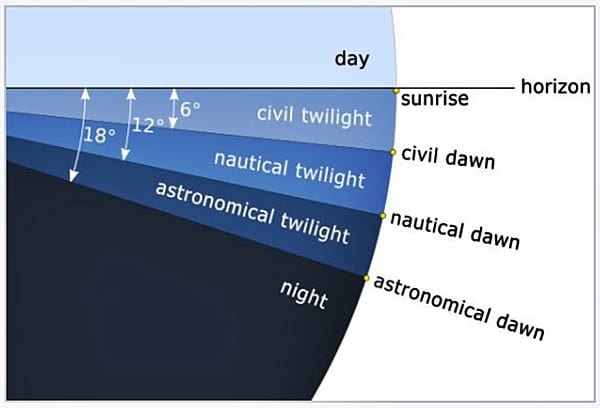
- Civil Twilight: The center of the body of the Sun lies between the horizon and 6o below the horizon. At this time you can still see things clearly without the need for extra illumination.
- Nautical Twilight: The center of the body of the Sun lies between 6o and 12o below the horizon. Objects become harder to see and appear in silhouette. The brightest stars begin to be visible in the night sky.
- Astronomical Twilight: The center of the body of the Sun lies between 12o and 18o below the horizon. It is completely dark and the stars are clearly visible in the night sky.
As an aside, recall that the Sun has a diameter of about 34′ of arc in the sky. In a previous post we say a chart of Masha’allah in which he notes the the Sun at 0 Aries 11 was considered a 7th house planet where the point opposite the Ascendant lay at 29 Pisces 39. In this case, the center of the Sun which has a diameter of 34′ of arc in the sky. If so, the body of the Sun lies partly in Pisces and partly in Aries. In fact, the body of the Sun extends from 29 Pisces 54′ to 0 Aries 28′. Thus, the Sun lies in the 7th sign from the Ascendant and also in the whole degree of the Descendant, and on this basis could be considered a 7th house planet.
Let’s return to Sahl for a moment and his Fifty Judgments. Sahl rendered Ptolemy’s idea about the 5-degree rule as follows in his Judgment 44 (Dykes translation, bold and italics mine):
“If a planet were in the beginning of a sign, it will be weak until it is made firm in it and walks through it by 6o [the period of civil twilight before sunrise]. And a planet does not fall from the angles except after 5o. For example, if the angle were in the 10th degree of Aries, every planet which is less than 5o [of Aries] is cadent and not thought to be in the angle.”
It seems to me that these ancient astrologers were deriving their notions of strength and influence with respect to the Ascendant from the analogy with sunrise and the gradual increase in light in the twilight period before sunrise. In astronomy civil twilight in which there is enough light to get things done even before the sun reaches the horizon is a period of 6o from the horizon. If we allow that each degree of the Ascendant corresponds to about 4 minutes on the clock, this corresponds to a period of 6 x 4 or 24 minutes of functional light before the sun actually conjoins the horizon.
An interesting fact is that the amount of usable light just prior to dawn varies with one’s proximity to the Equator. The further south you are, the more light that is available to you to get things done. For example, at the March Equinox, in:
- Quito, Ecuador (latitude 0), nautical twilight starts 20 minutes after sunset,
- Key West, Florida (latitude 24N), nautical twilight starts 23 minutes after sunset
- Kansas City (Latitude 39N), nautical twilight starts 26 minutes after sunset
- Anchorage, Alaska (latitude 62N), nautical twilight starts about 44 minutes after sunset.
What we see from this is that nautical twilight at the Equator lasts about 20 minutes, which corresponds to 5o at the Equator. Ptolemy made use of the arc traveled both on the equator on on the ecliptic and also made extensive use of ascensional times. It may be that for this reason he chose 5o as the period of influence to the eastern horizon (where the sun rises).
I have already mentioned an argument for applying the 5-degree rule to the other angular cusps. Is the a theoretical justification for applying it to intermediate houses? The answer may lie in the Hellenistic concept of Lots, which are usually projected from the Ascendant. In other words, the distance measured in arc along the ecliptic between two points or planets is projected from the degree of the Ascendant to produce the Lot.
With this in mind, I conjecture that Ptolemy reasoned more or less as follows in analyzing the length of life:
- The Ascendant (eastern horizon) is analogous to sunrise and represents the life force of the native.
- The sign containing the Horoskopos (Ascendant) is the 1st house of the Whole Sign House (topoi) system.
- But the power of the Ascendant has its maximum effect within 5 degrees of the Horoskopos, which can lie anywhere from 0 to 30 degrees within the ascending sign.
- Therefore, to evaluate where the maximum life-giving force has effects in the chart we must use a different type of house system with the Ascendant as the cusp of the 1st house and the point lying 5 degrees before the Ascendant as the initial boundary of the 1st house.
- Because traditional houses (topoi) are based on 30-degree Whole Signs, this new “longevital” house system must also have houses of exactly 30 degrees each, and they will be patterned after the 1st longevital house with its cusp as the horoskopos and its initial boundary as 5 degrees before the horoskopos.
- Based on Whole Sign Aspects, the most effective houses will be those in major whole sign aspect to the sign of the 1st house.
- Because the Ascendant is so powerful with regard to longevity, the cusps of the other houses will be in exact degree-based aspect to the Ascendant degree.
- For example, because the 8th Whole Sign house from the Ascendant represents the death of the native, the cusp of the 8th longevital house will be the point that is exactly 210 degrees from the Horoskopokos. In other words, the cusp of the 8th will be like a Lot in which the distance from boundary of the 1st whole sign house to boundary of the 8th whole sign house is projected from the Ascendant, and the boundary of the 8th longevital house will be 5 degrees before that cusp because of its analogy with the powerful Ascendant.
The ideas in this post are, of course, preliminary and subject to change. However, I think it offers a potential theoretical justification for the use of the 5-degree rule at least in judging the length of life. It may be that the use of the 5-degree rule in horary charts by Sahl was his attempt to generalize Ptolemy’s more restricted use to other branches of astrology.
Addendum (27 Dec 2017): Antiochus of Athens and Equalization
Antiochus of Athens was a Hellenistic astrologer who published sometime between the late 1st and mid 2nd century AD. In Robert Schmidt’s translation (pp.32-33) Antiochus writes:
“Each of these 12 places obtains as its lot the 5 pre-ascended degrees and the 25 post-ascending degrees, if the squares should occur through ninety degrees.”
If the Asc and MC degrees are not exactly 90 degrees apart, then Antiochus advises us to divide the degree of angles into three to determine the number of degrees for each place, and then adding “the 5 degrees that have pre-ascended it”. This appears to be his description of the house system now attributed to Porphyry.
My understanding of this passage (which may or may not be correct) is that when the Asc and MC cardines are exactly 90 degrees apart, the first house begins 5 degrees before the Ascendant and all the houses are 30-degrees in length. Because the MC is 90 degrees from the Asc, the beginning of the 10th place will be 5 degrees before the MC.
It does not seem logical to me, however, that the places are calculated proportionate to the size of the quadrant but the 5 pre-ascending degrees are not also proportionately calculated.
To give an example:
Suppose the Asc lies at 0 Gemini and the MC lies 60 degrees away at 0 Aries, then each place should be 60 divided by 3 = 20 degrees of arc in length. Following his logic, the 5 pre-ascended degrees should be proportionately reduced to 2/3 of 5 = 3.33 degrees.
In this same example the IC lies at 0 Libra, and the 2nd place would be the size of that quadrant divided by 3, or 120 divided 3 = 40 degrees and the 5 pre-ascending degrees would be proportionately increased by 4/3 = 6.66 degrees.
In other words, it doesn’t seem logical that the size of each place would vary according to the quadrant it is in but the 5 ascending degrees would remain constant regarding of the varying sizes of the quadrants.
In Masha’allah’s chart above, the MC lies at 21 Pisces 30 and the Descendant at 8 Capricorn. The size of this quadrant containing the 10th place extends from 8 Cancer (the Ascendant) to 21 Pisces 30 (the MC). This quadrant is 106.5 degrees. Dividing this figure by 3 we get 35.5 degrees. Proportionately, the 5 pre-ascended degrees is then equivalent to 35.5/30 times 5 or 5 deg 55 min of arc. Thus the 1st house would begin 5 deg 55 min above the Asc and the 10th house would begin 5 deg 55 min before the degree of the MC.

Hello Mr. Louis. Do you currently offer horary reports, please?
From section 24 paragraphs 20 and 21 of the Geographia of Ptolemaeus:
“But in order that the longitude is commensurate with the latitude … let us place eighteen meridians, each occurring every third part of an equatorial hour, to fill completely the whole of the longitudes encompassing the semicircles … we will take (from out of each of these three parallels) segments equivalent to one third or five degrees.”
Note that a 5º orb in longitude is equivalent to 2º in declination: 1º orb in longitude is equivalent to 24′ in declination.
Ptolemy notes (in the Geographia, not in the Tetrabiblos) in order for longitude to be (in an ideal sense) commensurate with latitude it is necessary to take segments equivalent to one third of an equinoctial hour (twenty minutes on the clock).
In Appendix B of his book Classical Scientific Astrology, George Noonan writes:
“One of the primary diurnal effects that must be accounted for is the heliacal rising of the stars and planets. But due to the refraction of the atmosphere and the large apparent size of the Sun with respect to the stars, a star may be obscured in its heliacal rising. Only by subtracting 5 degrees from the horoscope (ASC) will all heliacal risings be included within the first locus as is necessary. Again, remember that classical astrology uses observational astronomy as a tool.”